70-爬楼梯

70-爬楼梯

  • 题目描述

    • 假设你正在爬楼梯。需要 n 阶你才能到达楼顶。每次你可以爬 1 或 2 个台阶。你有多少种不同的方法可以爬到楼顶呢？

  • 解题思路：

    • 1阶 1种
    • 2阶 2种
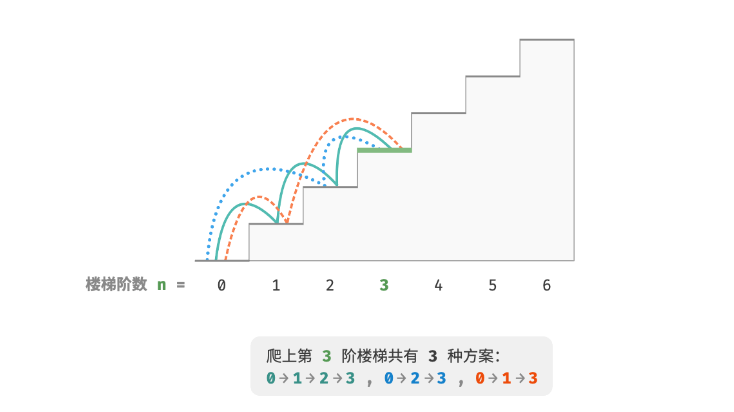
    • 3阶 3种

  • 步骤

    1. dp数组以及下际的含义：
      dp[i]:达到i阶有dp[i]种方法
    2. 递推公式
      dp[i] = dp[i-1] + dp[i-2]
    3. dp数组如何初始化
      dp[1] = 1; dp[2] = 2;尽量不初始化dp[0]，因为题目要求是正整数
    4. 遍历顺序
      从前向后遍历
      注意：很多动规的题目是从后往前遍历的
    5. 打印数组

  • 代码

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    class Solution {
    public:
        int climbStairs(int n) {
            if(n<=1) return n;
            vector<int> dp(n+1);
            dp[1] = 1;
            dp[2] = 2;
            for(int i = 3; i <= n; i++){
                dp[i] = dp[i-1] + dp[i-2];
            }
            return dp[n];
        }
    };
    • 时间复杂度：O(n)
    • 空间复杂度：O(n)

优化空间复杂度

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
class Solution {
public:
    int climbStairs(int n) {
        if(n <= 1) return n;
        int dp[3];
        dp[1] = 1;
        dp[2] = 2;
        for(int i = 3; i <= n; i++){
            int sum = dp[1] + dp[2];
            dp[1] = dp[2];
            dp[2] = sum;
        }
        return dp[2];
    }
}